FORCES & THEIR EFFECTS
Force - any influence which can distort, produce stress in, or alter the motion of a body of matter; force produces an effect on the shape, motion, direction, and speed of mass.
-
vector quantity
-
SI Unit is Newton (N)
-
Compression of an object - force influencing shape
-
lightly squeezing an elastic ball will cause a distortion in its form
-
squeezing a balloon will likely change its shape from a tear-drop-like figure to a figure resembling two awkward balls (see Fig. 1)
-
-
Blocking a moving object's path - force influencing motion
-
if a goalkeeper were to block a soccer ball from entering the net, they are changing the motion of the ball by reducing its speed to equal or almost equal to 0 (see Fig. 2)
-
-
Hitting an object - force influencing direction
-
if a baseball player were to hit the baseball with the bat, they would be changing the direction of the ball (see Fig. 3)
-
-
Pushing an object - force influencing speed
-
if a bottle is rolling on a flat surface, and it suddenly pushed forward, it will move at a faster pace than before
-
There are two key categories of forces:
-
Contact forces - forces that occur while two (or more) objects are in direct physical contact, e.g., friction.
-
Non-contact forces - forces that occur at a distance, without physical contact (these are also known as distant forces), e.g., gravitational force
DIFFERENT TYPES OF FORCES/FORCE TERMINOLOGY
-
Normal force - a contact force exerted by all objects which is perpendicular to the surface of the objects (see Fig. 4)
-
Friction - the force between objects in contact which acts opposite to the direction of movement, slowing down motion; frictional force depends on the texture of the surfaces in question (every surface has its own friction coefficient for both static and dynamic friction; in general, rough texture means more friction)
-
Static friction - the force that prevents stationary objects from moving
-
Kinetic friction - the force that acts against an object's motion
-
Drag force - the resistive force experienced by a body moving through a fluid (gas or liquid), e.g., air resistance, which slows down motion & works at a greater magnitude with larger masses
-
-
Tension - the general pulling force exerted by strings, ropes, fibers and cables
-
Applied force - a general term for any contact force
-
Weight - a force which acts on all matter within gravitational fields, can be defined as the product of gravitational field strength (N/kg) and an object's mass (kg)
-
Resultant force - the single force that results from two or more combined forces; can be found mathematically (using algebra) or geometrically (using the parallelogram rule)

Fig. 1: Compressed balloon.

Fig. 2: Goalkeeper catching a ball.

Fig. 3 - Baseball player striking ball.
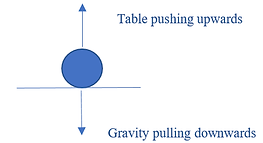
Fig. 4 - Normal force demonstration.
CALCULATING RESULTANT FORCES
Parallelogram rule
-
Draw two lines (vectors) from a point ‘O’ to represent two forces
-
Ensure that the direction and length of these vectors are proportional to those of the exact forces being represented
-
Use a protractor to ensure that the angles the vectors make are the same as the angles the forces make with a relative surface or direction
-
Choose a scale ratio that can be used to represent the magnitude of the force as the length of the vector
-
-
Draw two more lines starting at the ends of the two vectors to complete the parallelogram
-
Draw a diagonal from point 'O' to the convergence of the second pair of lines
-
Calculate the direction and magnitude of this vector - this is the resultant force
FORCES IN CIRCULAR MOTION
When objects are moving in circular paths, there are several forces at play which wouldn't necessarily be present in linear motion.
-
Centripetal force - the net force acting on the object in motion, which will always be pulling the object inwards towards the center of its circular trajectory
-
if the moving object is attached to a string or rod (or other object), the tension force experienced by the string/rod will be the centripetal force
-
the moving object will be constantly accelerating since its velocity is also constantly changing (velocity is a vector quantity affected by direction - non-linear direction means change in velocity even if the speed does not change)
-
can be quantified with F = mv^2/r
-
F - centripetal force (N)
-
m - mass (kg)
-
v - velocity (m/s)
-
r - radius of circular trajectory (m)
-
-
-
Centrifugal force - the fictitious force that is equal in magnitude but opposite in direction to the centripetal force; the force that pushes an object in a circular trajectory outwards from the center
-
this force does not actually exist, and if the circular motion stops, the object will continue to move in a straight path tangent to its last position in the circular path - this occurs due to inertia.
-
FORCES IN ROTATIONAL MECHANICS
In a linear system, force provides acceleration; in a rotational system, torque (which requires a causal force) provides angular acceleration.
Torque - the measure of a force that can cause an object to rotate about an axis; the rotational equivalent of a linear force. Torque can be understood when opening a door; a smaller force is required to open it when it is applied further from the hinges. In this case, the hinge is the rotational axis, and the door is the moment arm.
-
vector quantity
-
SI unit is Newton-meter (Nm)
-
can be quantified with T = F*r*sin(θ)
-
T - torque (Nm)
-
F - force vector (N)
-
r - length of moment arm, or from axis of rotation to the point of application of force (m)
-
θ - angle between force vector and moment arm (degrees)
-
Torque is different from centripetal force because torque causes rotation about an axis, whereas centripetal force changes the direction of a moving object.
MOMENTUM & IMPULSE
Momentum - the product of any moving object's mass and velocity; a quality that results from motion
-
vector quantity
-
SI unit is kilogram-meters per second (kg*m/s)
-
can be quantified with p = mv
-
p - momentum (kg*m/s)
-
m - mass (kg)
-
v - velocity (m/s)
-
Impulse - change in momentum; the product of force and time
-
vector quantity
-
SI unit is Newton-second (Ns)
-
can be quantified with Δp = m*Δv OR Δp = m*a*Δt OR Δp = F*Δt
-
Δ - delta, signifying 'a change in'
-
p - momentum (kg*m/s)
-
m - mass (kg)
-
v - velocity (m/s)
-
a - acceleration (m/s^2)
-
t - time (s)
-
F - force (N)
-
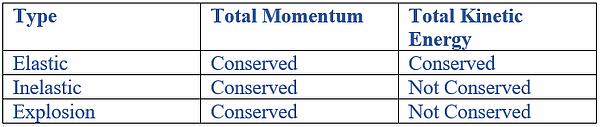
Law of conservation of momentum - when two or more objects in a system act on each other (exchange direct contact, e.g. collide), the total momentum of the system remains constant, provided no external forces are acting on it
-
this does not necessarily mean that the momentum of the individual objects will not change; just that the total momentum before the collision will be equal to the total momentum after the collision
There are multiple types of collisions in which the law of conservation of momentum may apply. These are listed in the table below.
Before the explosion, the total momentum of the bomb is zero. Upon the explosion, the bomb will crack into fragments and accelerate into varying, random directions. The vector sum of the moments of the fragments is zero, thus the momentum is conserved